Observable Quantities

According to folklore, the physicist Richard Feynman, who boasted about his mathematical intuition, was once asked by some trickster mathematicians whether it is possible to break the unit ball into finitely many disjoint pieces, and re-arrange them by rigid motions to form two unit balls. Such a procedure is known as a “paradoxical decomposition”. Feynman answered that it is impossible. The reasoning Feynman likely used is this:

The volumes of the pieces must sum to 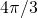$4 \pi/3$ , the volume of the unit ball.
Rigid motions won’t change the volumes of the pieces, so after re-arranging the pieces, their volumes still sum to $4\pi/3$ .
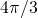Thus the re-arranged figure cannot be two copies of the unit sphere, since that has volume 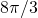$8\pi/3$ , which is more than the sum of the volumes of the re-arranged pieces.

However, it turns out if you accept axiom of choice, you can prove it is possible to do it! This is known as the Banach Tarski Paradox. Feynman apparently responded that his answer was still correct, since the pieces given in the mathematician’s construction are physically impossible.

In fact, Feynman was right: the pieces in the Banach-Tarski construction cannot be measurable: they cannot be consistently assigned a volume.

Many have suggested because of its paradoxical consequences that we should reject the axiom of choice. On the other hand, the axiom of choice is a very simple principle, and many find it to be obviously true. The axiom of choice says that if you have an indexed collection of non-empty sets $(A_i : i \in I)$ , you can find an indexed collection of elements $(a_i : i \in I)$ where each $a_i$ belongs to $A_i$ . Imagine, if you will, a collection of boxes of socks. The axiom of choice says you can choose one sock from every box. Results by Kurt Gödel and Paul Cohen established that the axiom of choice is independent of (can neither be proven or disproven from) the other axioms of set theory, so any argument to accept it or reject it is going to be philosophical rather than mathematical.

At this point you are probably wondering, what does all this have to do with observable quantities? Well, one important principle of science is empiricism: the adequacy of a scientific theory rests ultimately on its consistency with our observations. In a sense which can be precisely defined, there is no experiment anyone could conduct to give evidence for or against the axiom of choice. In what follows, we want to describe a connection between constructivism in mathematics, and empiricism in the sciences. Intuitively, the kinds of properties which we can gain empirical knowledge of ought to be constructible, with properties at the lowest levels of a hierarchy of constructibility corresponding to properties which can be effectively verified or falsified by observation. If we need to use the axiom of choice to prove that a particular mathematical object exists, it is very far from constructible, and thus, one could argue, should play no role in a scientific theory.

Connecting Science with Mathematics

One way we can connect mathematics to empirical science is to imagine that every scientific experiment is broken up into a collection of sub-experiments with binary (“yes” or “no”) outcomes. For example, suppose you want to measure voltage across two points in a circuit. You might first ask, “Is the voltage at most 32V?”. If the answer is yes, you ask, “Is it between 0V and 16V?”. If the answer is no, then it must be between 16V and 32V, so your next question will be “Is it between 16V and 24V?”. By asking finer and finer binary questions, you can narrow down the voltage to any level of precision you like. By the way, this process I just mentioned is pretty much how an ADC (analogue-to-digital converter) works: it’s a circuit which takes in a voltage, and gives you a sequence of binary bits representing the voltage.

In a complicated experiment, we may have many quantities we are trying to control and measure. But in principle, any such experiment will ultimately result in a finite collection of bits, which we can think of as the contents of the scientist’s lab notebook. Even if a scientist is using analogue equipment, when they type up a paper in LaTeX and submit it to publication, it has been converted into digital information. We could even totally remove the scientists from the equation, by imagining that we have a robot outfitted with a large collection of sensors which is controlled by a computer. We could program this robot to conduct a complicated experiment, involving building specialized equipment, performing intermediate tests for calibration, etc. In fact, the code controlling such a scientific robot would be considered by many to be the ultimate standard for describing the methodology of an experiment: replication would be a breeze!

In any case, we can in principle describe the setup of the experiment with some finite number of bits, and the outcome of the experiment will be some finite number of bits. Then a scientific hypothesis could be expressed mathematically by a partial function $F$ which takes as input some sequence of bits $\sigma$ describing an experimental setup, and outputs a sequence of bits $F(\sigma)$ describing the experimental outcome. An example of such function would be a function that takes a description of the positions and velocities (up to a margin of error) of a bunch of pool balls, and tells you what their positions and velocities (up to another margin of error) will be 10 seconds from now.

If we are careful with the way we set up the encoding of information, we can arrange these descriptions of experimental setups in a partial order: we will say $\sigma \leq \tau$ if $\tau$ describes an experimental setup which is consistent with everything $\sigma$ says about it. In the pool ball example, $\tau$ might describe the positions and velocities up to a smaller margin of error than $\sigma$ . We can do the same for experimental outcomes. We can now describe two topological spaces: a space of experimental setups $\mathcal{S}$ , and a space of experimental outcomes $\mathcal{O}$ . $\mathcal{S}$ will be the collection of all maximally consistent sets of descriptions of experimental setups, while $\mathcal{O}$ will be the collection of all maximally consistent sets experimental outcomes. That is, a point in $\mathcal{S}$ will be a collection of the form $\{\sigma_{i} : i \in I\}$ such that adding even a single new $\sigma$ would make it inconsistent. A base for the topology of $\mathcal{S}$ will be $\big\{ \{ s \in \mathcal{S} : \sigma \in s\} : \sigma \text{ is a description of an experimental setup} \big\}$ . Likewise for $\mathcal{O}$ . If we had a complete, deterministic physical theory, and the laws of physics were continuous, then the corresponding function $F$ would determine a total continuous function $f: \mathcal{S} \rightarrow \mathcal{O}$ .

If our theory is not deterministic, we could still represent it mathematically, we’d just think of $\mathcal{O}$ as a space of probability distributions over outcomes instead. Because of the construction of $\mathcal{S}$ and $\mathcal{O}$ , both $\mathcal{S}$ and $\mathcal{O}$ could be represented as quotients of Baire space, $\omega^{\omega}$ , so ultimately, our functional model (relating experimental setups to experimental outcomes, or probability distributions over experiment outcomes), can be represented using a function $f : \omega^{\omega} \rightarrow \omega^{\omega}$ . This brings us into the realm of an area of mathematics known as descriptive set theory. If we believe that the laws of physics are continuous, we should expect that this function $f$ should be continuous: if $O$ is an open set of outcomes, then $f^{-1}(O) = \{x : f(x) \in O\}$ should be open as well.

Connecting Science with Mathematics

Leave a Reply Cancel reply