Ancient Greek philosophers used to study mathematics, because mathematical thinking provided an ideal model of philosophical thought, free of the complications of hairier subjects in philosophy like ethics. Plato’s dialogue Meno, for example, uses a mathematical demonstration to probe the nature of knowledge. Although at times mathematics can seem like it has no connection to the real world, occasionally a deep understanding of some mathematical concepts can give clarity to our ordinary ways of thinking. One of the most beautiful examples of this comes from linear algebra.
To set the stage, we should first recall the phrase, “the map is not the territory”.
A map is not the territory it represents, but, if correct, it has a similar structure to the territory, which accounts for its usefulness.
— Alfred Korzybski
In the context of linear algebra, this concept is important for students to understand when they learn the difference between a vector and the coordinates of that vector. The reason students get confused about this in the first place is because usually the first vector spaces they are exposed to are vector spaces like ![]() , where vectors are usually written out with notation like
, where vectors are usually written out with notation like 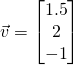 . In this special case, it is okay to identify the vector
. In this special case, it is okay to identify the vector ![]() with a triple of real numbers, because for
with a triple of real numbers, because for ![]() there is a canonical coordinate system (due to the way
there is a canonical coordinate system (due to the way ![]() is constructed). In this special case, vectors really are their own coordinates (i.e., the map is the territory)!
is constructed). In this special case, vectors really are their own coordinates (i.e., the map is the territory)!
When the Map is not the Territory
However, this breaks down once you consider other vector spaces like ![]() , the space of polynomials of degree at most two. A polynomial of degree at most two is a function which can be written in the form
, the space of polynomials of degree at most two. A polynomial of degree at most two is a function which can be written in the form ![]() , with
, with ![]() ,
, ![]() , and
, and ![]() real numbers. It may be tempting to then identify
real numbers. It may be tempting to then identify ![]() with the triple of numbers
with the triple of numbers ![]() , but this would be a mistake! For one, although it is possible to expand all polynomials of degree at most two in terms of
, but this would be a mistake! For one, although it is possible to expand all polynomials of degree at most two in terms of ![]() ,
, ![]() , and
, and ![]() , they can also be expanded in terms of
, they can also be expanded in terms of ![]() ,
, ![]() , and
, and ![]() . If we take a polynomial like
. If we take a polynomial like ![]() , we could re-express it, just as validly, as
, we could re-express it, just as validly, as ![]() . Indeed, a little basic algebra shows that:
. Indeed, a little basic algebra shows that:
![]()
This means the same polynomial ![]() , depending on which basis we expand it in terms of, could either be represented as
, depending on which basis we expand it in terms of, could either be represented as ![]() or
or ![]() (among others). If Alice were to use the basis
(among others). If Alice were to use the basis ![]() and Bob were to use the basis
and Bob were to use the basis ![]() , and both were to identify
, and both were to identify ![]() with its coordinate vector, Alice and Bob would arrive a contradiction by the chain of equalites:
with its coordinate vector, Alice and Bob would arrive a contradiction by the chain of equalites:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3 \\ 4 \\ 1 \end{bmatrix} = p(t) = \begin{bmatrix} 3 \\ 10 \\ 8 \end{bmatrix}\]](https://moody.industries/blog/wp-content/ql-cache/quicklatex.com-575c24d5b253346514ee895126f584d6_l3.png)
Resolving the Contradiction
To resolve this apparent contradiction, all we have to do is recognize that different people may map the same territory in different ways. Alice might describe the polynomial ![]() using the coordinates “
using the coordinates “![]() “, and Bob might describe
“, and Bob might describe ![]() using the coordinates “
using the coordinates “![]() “. Both are equally valid descriptions of
“. Both are equally valid descriptions of ![]() , but they are descriptions in different descriptive frameworks (i.e., in different languages).
, but they are descriptions in different descriptive frameworks (i.e., in different languages).
One way of formalizing this idea is to use a special notation for “description of an object with respect to a given descriptive framework”. If ![]() is an object (like a polynomial), and
is an object (like a polynomial), and ![]() is a descriptive framework (like Alice’s coordinate system), then we use the notation
is a descriptive framework (like Alice’s coordinate system), then we use the notation ![]() to denote the description of object
to denote the description of object ![]() in descriptive framework
in descriptive framework ![]() . In this notation, we can see how the contradiction above no longer goes through:
. In this notation, we can see how the contradiction above no longer goes through:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3 \\ 4 \\ 1 \end{bmatrix} = [p(t)]_{\mathcal{A}} \neq [p(t)]_{\mathcal{B}} = \begin{bmatrix} 3 \\ 10 \\ 8 \end{bmatrix}\]](https://moody.industries/blog/wp-content/ql-cache/quicklatex.com-d95ba521047d06bd6659a0a24549fd0c_l3.png)
We have no more reason to believe that ![]() (the description of
(the description of ![]() in Alice’s descriptive framework) is the same as
in Alice’s descriptive framework) is the same as ![]() (the description of
(the description of ![]() in Bob’s descriptive framework) than we have to believe that the word used to describe shoes in English is the same as the word used to describe shoes in French. Of course, it may happen by sheer coincidence that the descriptions of an object in two different languages are the same, but this is not to be expected.
in Bob’s descriptive framework) than we have to believe that the word used to describe shoes in English is the same as the word used to describe shoes in French. Of course, it may happen by sheer coincidence that the descriptions of an object in two different languages are the same, but this is not to be expected.
However, that doesn’t mean that the descriptions of objects in two different descriptive frameworks bear no relation at all. Indeed, if we consider the Alfred Korzybski quote above, if we know that ![]() has a similar structure to the territory, and
has a similar structure to the territory, and ![]() has a similar structure to the territory, then
has a similar structure to the territory, then ![]() and
and ![]() should have similar structure to each other!
should have similar structure to each other!
Deriving a Translation Rule
One way to capture the similarity in structure between two descriptive frameworks is to describe a translation between them. Using Alice and Bob’s descriptive frameworks for polynomials of degree at most two from earlier, it turns out we can derive a straightforward algebraic translation from ![]() to
to ![]() for any polynomial
for any polynomial ![]() of degree at most two. Let’s derive this now.
of degree at most two. Let’s derive this now.
First, let’s suppose that ![Rendered by QuickLaTeX.com [p(t)]_{\mathcal{A}} = \begin{bmatrix} a \\ b \\ c \end{bmatrix}](https://moody.industries/blog/wp-content/ql-cache/quicklatex.com-4ee0caf0ecaff92baafb146abe12b1f4_l3.png) . Then we can derive:
. Then we can derive:
![]()
But this means
![Rendered by QuickLaTeX.com \[[p(t)]_{\mathcal{B}} = \begin{bmatrix} a \\ 2a + b \\ a + b + c \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \\ c \end{bmatrix}\]](https://moody.industries/blog/wp-content/ql-cache/quicklatex.com-c19c56fbd072348839155cc18a202659_l3.png)
![Rendered by QuickLaTeX.com \[[p(t)]_{\mathcal{B}} = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix}[p(t)]_{\mathcal{A}}\]](https://moody.industries/blog/wp-content/ql-cache/quicklatex.com-63c67ed749da84012283dd75bcbcc099_l3.png)
What we notice in this case is that there is a linear relationship between ![]() and
and ![]() . In the context of linear algebra, the translation rule between
. In the context of linear algebra, the translation rule between ![]() and
and ![]() is known as a change of coordinates, and it is described by an invertible matrix.
is known as a change of coordinates, and it is described by an invertible matrix.
An Exercise to Test Your Understanding
Before reading on, try to answer the following question using your understanding of linear algebra and the Alfred Korzybski quote above:
Why is the relationship between ![]() and
and ![]() linear?
linear?
If you are stuck, here’s a hint: Alice and Bob’s coordinate systems are both linear coordinate systems. That is, ![]() and
and ![]() (and likewise for
(and likewise for ![]() ).
).
Figured it out? If not, here’s the answer. The functions ![]() and
and ![]() are invertible linear maps. Thus the map
are invertible linear maps. Thus the map ![]() is linear (and invertible). Now tracing back definitions,
is linear (and invertible). Now tracing back definitions, ![]() , so
, so ![]() is indeed the translation from
is indeed the translation from ![]() descriptions/coordinates to
descriptions/coordinates to ![]() descriptions/coordinates. In plain English: the relationship between
descriptions/coordinates. In plain English: the relationship between ![]() and
and ![]() is linear because the relationships between
is linear because the relationships between ![]() and
and ![]() and between
and between ![]() and
and ![]() are both linear.
are both linear.
Picturing What’s Going On
The following diagram explains what’s going on when we translate between ![]() and
and ![]() coordinates, and vice versa:
coordinates, and vice versa:
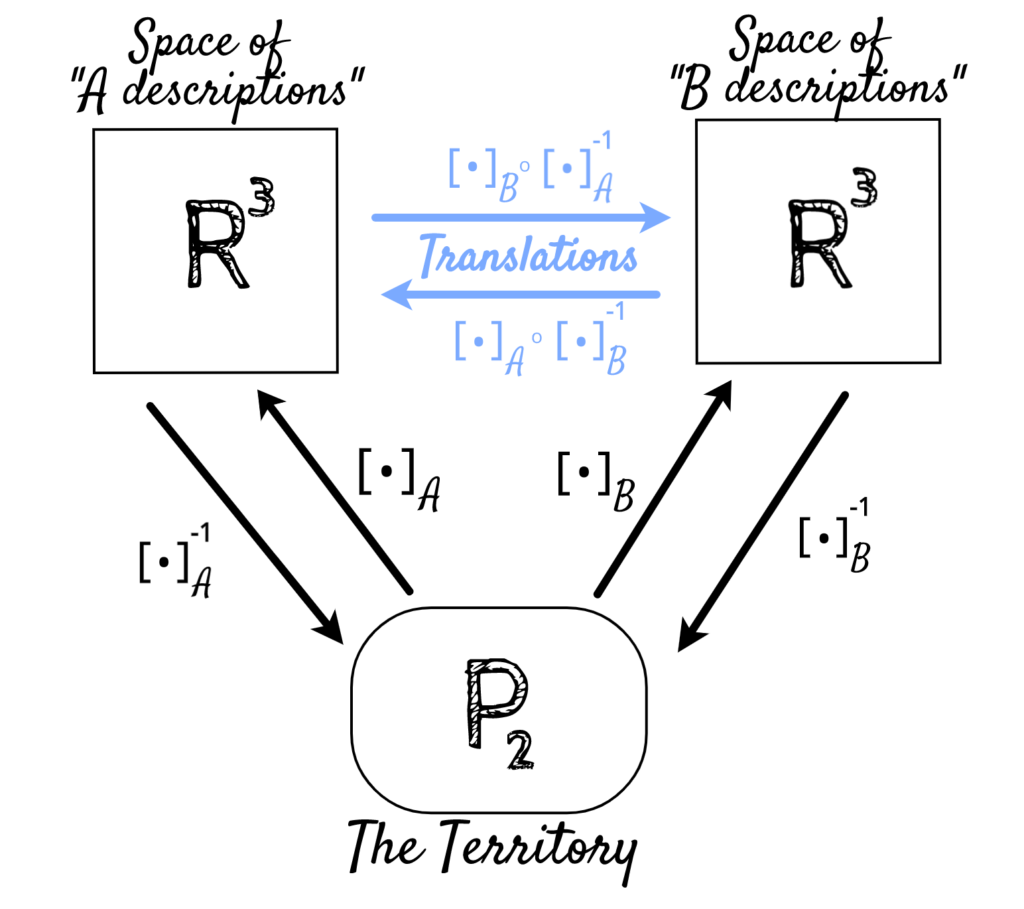
This diagram applies far more general than you might expect. If we replace ![]() with an arbitrary domain (corresponding to a territory), and the two copies of
with an arbitrary domain (corresponding to a territory), and the two copies of ![]() with arbitrary spaces of descriptions, then the blue formulas for translation between
with arbitrary spaces of descriptions, then the blue formulas for translation between ![]() and
and ![]() descriptions are still valid, so long as
descriptions are still valid, so long as ![]() and
and ![]() are bijective functions. Since
are bijective functions. Since ![]() and
and ![]() are maps from objects of the domain to descriptions, this is just another way of saying that every object in the domain has a unique
are maps from objects of the domain to descriptions, this is just another way of saying that every object in the domain has a unique ![]() -description (resp.
-description (resp. ![]() -description), and every
-description), and every ![]() -description (resp.
-description (resp. ![]() description) corresponds to a unique object in the domain. Although this is not true for natural languages (because sometimes descriptions fit more than one object, and some objects have many different descriptions), it is often true for artificial languages / descriptive frameworks.
description) corresponds to a unique object in the domain. Although this is not true for natural languages (because sometimes descriptions fit more than one object, and some objects have many different descriptions), it is often true for artificial languages / descriptive frameworks.
What’s special in the case of linear algebra is just that these functions ![]() and
and ![]() are invertible linear maps, which implies all the arrows in this diagram are invertible linear maps.
are invertible linear maps, which implies all the arrows in this diagram are invertible linear maps.

