Hypergame Paradox, Set-Theoretic Comprehension, and Cantor’s Argument

We can represent a single-player game as a tree, where each node corresponds to a state of the game, and each branch leaving a node corresponds to one of the possible moves you can make.

Green nodes correspond to a victory, red nodes to a loss.

Note that we could also represent two-player games in this way: player 1 makes a move at even levels of the tree, and player 2 makes a move at odd levels of the tree. We call a game finite if its tree has no infinite paths, i.e. if the game must eventually end no matter what sequence of moves is made. A finite game need not have only finitely many possible states. Here’s an example of a finite game where there are infinitely many possible first moves:

For the first move, choose a natural number $n_1$
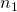
For the 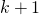$k+1$ -st move, pick a natural number 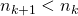$n_{k+1} < n_k$ which divides 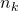$n_k$ , if possible.
The game ends when you reach 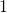$1$ (which has no factor strictly less than itself).

If the first move is to choose $n_1 = 10^{10^{10^{10^{10^{10^{10}}}}}$ , this game could go on for a very long time (longer than the age of the universe). You can find arbitrarily-long finite sequences of moves in this game. But since the sequence $n_1, n_2, n_3, \dots$ is always strictly decreasing, and the natural numbers are well-founded, it must eventually reach $1$ and terminate.

Now let’s define a new game called hypergame. Here are the rules:

In the first move of hypergame, choose a finite game 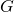$G$ to play.
In the second move of hypergame, play one of the possible first moves of $G$ .
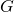In subsequent moves, keep playing valid moves of 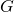$G$ until you reach the end. At this point, hypergame ends.

We might wonder: is hypergame a finite game? Well, once we’ve made our first move, all subsequent moves of hypergame are just moves in some finite game. We know all sequences of moves in a finite game eventually terminate, so all sequences of moves in hypergame must eventually terminate too (just perhaps one move later than the corresponding sequence of moves in the finite game chosen in the first move).

There’s also a geometric way of seeing this. We can build hypergame by first taking the collection of all game trees of finite games, and putting a common root below them. The fact we are using is just that if you take a collection of trees, none of which have an infinite path, and add a common root to all of them, this new tree still has no infinite path.

This sounds all fine and dandy: hypergame is a finite game. But then a valid first move of hypergame is to choose to play the game hypergame! And a valid first move of that game (second move of our original game) is to choose to play the game hypergame. And a valid first move of that game (third move of our original game) is to choose to play the game hypergame, and so on ad infinitum. This means the game tree for hypergame has an infinite path, so hypergame is not finite after all. But this is a contradiction!

This is known as the hypergame paradox. You might notice a similarity to Russell’s paradox. This is far from coincidental! Sets can be represented as trees, where the nodes immediately above a given node in the tree correspond to the elements of the set corresponding to that node. The axiom of foundation says that there are no infinite paths: every sequence of elements $x_1 \ni x_2 \ni x_3 \ni \dots$ must eventually terminate.

The way we can resolve this paradox is by noticing that we made use of unrestricted comprehension in our definition of hypergame (the very same principle which leads to Russell’s paradox). Specifically, we formed the second level of nodes in the game tree for hypergame by including a node for every game which happens to be finite. But in modern set theory based on the Zermelo-Fraenkel axioms, we are only allowed to do this if we know in advance that the collection of all games form a set (this is called restricted comprehension).

This brings us to an interesting question: what happens if we try to modify hypergame to use only restricted comprehension? Here’s an idea:

Given a set $X$ , we define the set $\mathcal{G}(X)$ to be the set of games whose set of nodes is a subset of $X$ . Now we define a game $hypergame_{\kappa}$ for $\kappa$ a cardinal as follows:

In the first move of 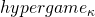$hypergame_{\kappa}$ choose a finite game in 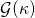$\mathcal{G}(\kappa)$ to play.
In the second move of 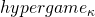$hypergame_{\kappa}$ play one of the possible first moves of $G$ .
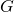In subsequent moves, keep playing valid moves of 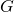$G$ until you reach the end. At this point, 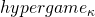$hypergame_{\kappa}$ ends.

Now, our previous analysis still goes through: $hypergame_{\kappa}$ is a finite game. But it cannot be represented as an element of $\mathcal{G}(\kappa)$ : otherwise, a valid first move of $hypergame_{\kappa}$ would be to play $hypergame_{\kappa}$ and we’d reach a contradiction as before.

What have we accomplished? Well, every element of $\mathcal{G}(\kappa)$ can be represented as a subset of $\kappa \times \kappa$ (corresponding to the directed edge relation of the game tree). We know that $\kappa \times \mu = max(\kappa, \mu)$ when $\kappa$ and $\mu$ are infinite cardinals. This means $|\mathcal{G}(\kappa)| \leq |\mathcal{P}(\kappa \times \kappa) |= |\mathcal{P}(\kappa)|$ when $\kappa$ is an infinite cardinal (where $\mathcal{P}(X)$ is the powerset, or set of subsets, of X). On the other hand, each game in $\mathcal{G}(\kappa)$ has at most $\kappa \times \kappa = \kappa$ many edges, so there are at most $\kappa \times |\mathcal{P}(\kappa)| = max(\kappa, |\mathcal{P}(\kappa)|)$ many nodes in $hypergame_{\kappa}$ . But since we’ve shown $hypergame_{\kappa}$ cannot be represented as a game with at most $\kappa$ nodes, we must have that $max(\kappa, |\mathcal{P}(\kappa)|) > \kappa$ . In other words, $|\mathcal{P}(\kappa)| > \kappa$ , which is the conclusion of Cantor’s Argument!

Hypergame Paradox, Set-Theoretic Comprehension, and Cantor’s Argument

One response to “Hypergame Paradox, Set-Theoretic Comprehension, and Cantor’s Argument”

Leave a Reply Cancel reply